2.1 Tensors
: 20 minutes
We first recall from last chapter our hypothetical study of BMI, where we organized our sample in a (two-dimensional) matrix having three feature columns (weight, height, and age) and 25 rows each representing measurements from each of the 25 respondents.
| student | weight | height | age |
|---|---|---|---|
| student 1 | 153 | 68 | 46 |
| student 2 | 196 | 55 | 30 |
| … | … | … | … |
| student 3 | 163 | 58 | 26 |
Such data is called cross-sectional, since the features were measured at a particular point of time, say January 1, 2025. In order to make our toy study more involved, we now decide to collect data every day from January 1 to December 31. The data collected over the whole year may, for example, help us find temporal trends that may otherwise be obscured.
Now the question is how to store the acquired data efficiently? Instead of sparing 365 matrices each collected per day, we create a three-dimensional matrix, also called a tensor!
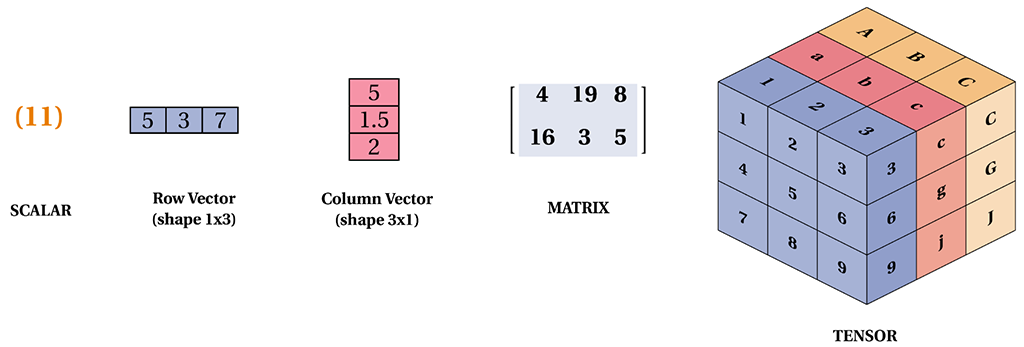
Definition
Tensors are higher-order matrices. Just as scalars are 0^{\textrm{th}}-order tensors, vectors are 1^{\textrm{st}}-order tensors, and matrices are 2^{\textrm{nd}}-order tensors, and so on.
Tensors are just containers of data. The order is chosen to match the design of the experiment. In the temporal version of our BMI study, the resulting tensor is 3rd-order.
We denote general tensors by capital letters with a special font face (e.g., \mathsf{X}, \mathsf{Y}, and \mathsf{Z}) and their indexing mechanism (e.g., x_{ijk} and [\mathsf{X}]_{1, 2i-1, 3}) follows naturally from that of matrices.
Order or Number of Axes
Number of axes of a tensor is also termed as the order or rank of the tensor.
Plainly speaking, the axes or order of the tensor is number of indices that will be required to access a specific element in the multi-dimensional array or tensor.

In our BMI study, the resulting tensor is 3rd-order or having three axes corresponding to date, respondent, and feature. Here, the dates are indexes along the first axis or axis=0; axis indices commonly start at 0. Along this axis, there are 365 matrices or 2nd-order tensors—each corresponding to a particular date. As a result, to access from the data tensor the measurement of a specific feature for a particular respondent on a given date, we need to specify three numbers. For example, (Aug 29, John Doe, Age) returns a number: the measured age of John Doe on Aug 29.
Shape of a Tensor
The shape of a an rth-order is a tensor of length r representing the dimensions the tensor has along each of respective axis.
In our BMI study, the shape of the data tensor shape is (365,25,3).
