9.1 Binary Logistic Regression

The binary classification problem assumes that the output set \mathcal{Y} has two order, discrete labels or classes: \mathcal{Y}=\{\tt 0, \tt 1\}; and, each label of each sample belongs to exactly one of them. Examples include predicting

admission to an academic program based on standardized test scores,
credit card default using their spending behavior,
breast cancer diagnosis, etc.

We use Binary Logistic Regression (a.k.a., Sigmoid Regression) to solve the binary classification problem.

Feature Vector

We assume there are d predictors (x_1, x_2, \ldots, x_d). For notational convenience with weights, we preppend 1 to the vector when denoting our feature vector, i.e., \bold{x}=(1, x_1, x_2, \ldots, x_d).

In case d=1, the problem is called univariate.

Model Assumptions

Recall that the underlying rule f is unknown to us, much like a “blackbox”. In binary logistic regression, we make two assumptions about the blackbox:

the conditional probability p(y = {\tt 1}\mid \bold{x}) follows the Bernoulli distribution¹ with mean \mu(\bold{x});
the conditional mean \mu(\bold{x}) is the sigmoid² of a linear function of \bold{x}, i.e., \mu(\bold{x})=\frac{1}{1+\exp(\bold{w}^T\bold{x})}.

¹ A random variable Z with two outputs \{\tt 0, 1\} is said to follow the Bernoulli distribution with mean \mu\in[0,1] if its probability density function: p(z)=\begin{cases}\mu,&\text{ if } z={\tt 1}\\ 1-\mu,&\text{ if }z={\tt 0} \end{cases}

² the sigmoid (S-shaped) function is denoted by \mathrm{sigm}(t)\colon\mathbb{R}\to\mathbb{R}. It maps the entire real line to the interval [0,1]; see Figure 26.1

The (d+1) weights w_0, w_1, \ldots, w_d are the parameters \pmb{\theta} of the model. Since the number of parameters does not grow with the size of the data, this is a parametric model.

function sigmoid(x, k=1, x0=0) {
  return 1 / (1 + Math.exp(-k * (x - x0)));
}

// Generate data points
data = {
  const points = [];
  for (let x = -10; x <= 10; x += 0.1) {
    points.push({ x: x, y: sigmoid(x, 1, 0) });
  }
  return points;
}

// Create the plot
Plot.plot({
  width: 700,
  height: 400,
  marginLeft: 60,
  marginBottom: 60,
  grid: true,
  x: {
    label: "t →",
    domain: [-10, 10]
  },
  y: {
    label: "↑ sigm(t)",
    domain: [0, 1]
  },
  marks: [
    Plot.line(data, {
      x: "x",
      y: "y",
      stroke: "#2563eb",
      strokeWidth: 3
    }),
    Plot.ruleY([0.5], { 
      stroke: "#94a3b8", 
      strokeDasharray: "4,4",
      strokeWidth: 1
    }),
    Plot.ruleX([0], { 
      stroke: "#94a3b8", 
      strokeDasharray: "4,4",
      strokeWidth: 1
    })
  ]
})

Figure 26.1

Model Distribution

Since, we are making a model assumption in terms of the conditional probability for the first time in this course, it deserves an explanation. For simplicity, assume the univariate case (d=1) with just one predictor, say x.

Mathematical Formulation

We now describe the mathematical formulation for the multivariate case with d\geq1 predictors x_1, x_2, \ldots, x_d.

Feature vector: \bold{x}=(1, x_1, \ldots, x_d)
Binary output: y={\tt 0}\text{ or }{\tt 1}
Model weights: \bold{w}=(w_0, w_1, \ldots, w_d)
w_0 is called the bias or intercept

As per our model assumption, we have

p({\tt 1}\mid\bold{x}; \bold{w})=\tfrac{1}{1+\exp(\bold{w}^T\bold{x})} =\tfrac{1}{1+\exp(w_0+w_1x_1+\ldots+w_dx_d)} \tag{26.1}

Prediction

Given a dataset \mathcal{D}=\{(\bold{x}_i, y_i)\}_{i=1}^N of size N from the blackbox f, we learn an approximation \hat{f} by learning the weights \bold{w}.

Here, each (boldfaced) input \bold{x}_i represents a vector (1, x_{i1}, x_{i2}, \ldots, x_{id}) and corresponding output y_i is either \tt 1 or \tt 0.

If \bold{w}^*=(w_0^*, w_1^*, \ldots, w_d^*) denotes our learned weights, we can write our learned probability distribution \hat{p}({\tt 1}\mid \bold{x};\bold{w}^*) =\frac{1}{1+\exp(w^*_0+w^*_1x_1+\ldots+w^*_dx_d)} \tag{26.2}

Then, we can predict the labeled or class of new data point with feature vector \bold{x} using the following threshold function: \hat{y}=\begin{cases} {\tt 1}&\text{ if }\hat{p}({\tt 1}\mid\bold{x};\bold{w}^*)\geq0.5 \\ {\tt 0}&\text{ if }\hat{p}({\tt 1}\mid\bold{x};\bold{w}^*)<0.5. \end{cases}

Optimization

Now, we turn our attention to finding the best or optimal weights, w.r.t. some notion of error. We use maximum likelihood estimator (MLE) to maximize the odds or probability of the occurrence of the given data \mathcal{D}.

Metrics for Classification

In regression, we used metrics like the Mean Squared Error (MSE) and \mathcal{R}^2 as metrics for “good of fit”. In classification, we use a different set of metrics:

Confusion Matrix
Accuracy
Precision, Recall, and F1-score

Confusion Matrix

In binary classification problem, the confusion matrix turns out be a 2\times2 matrix, which capture to what degree a classifier misclassifies the (training/test) data.

Using the convention that \tt 1=POSITIVE and \tt 0=NEGATIVE, we define:

\text{\color{green}True Positive} (TP): (as desired) an observation is classified by the classifier as POSITIVE while its original label was POSITIVE;
\text{\color{green}True Negative} (TN): (as desired) an observation is classified by the classifier as NEGATIVE while its original label was NEGATIVE;
\text{\color{red}False Positive} (FP): an observation is (mis)classified by the classifier as POSITIVE while its original label was NEGATIVE;
\text{\color{red}False Negative} (FN): an observation is (mis)classified by the classifier as NEGATIVE while its original label was POSITIVE;

Since the above cases are exhaustive, we have the following Venn diagram:

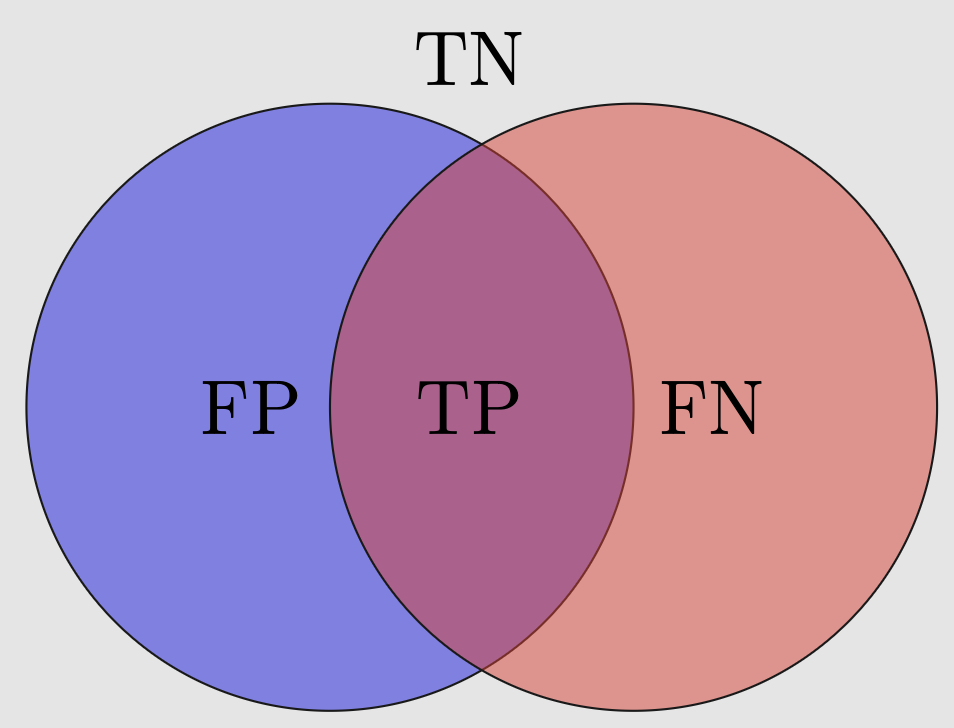
A yet better representation scheme is reporting the number of observations that fall into the above four cases as a matrix: the confusion matrix.

{
  const width = 500;
  const height = 500;
  const margin = 120;
  
  const svg = d3.create("svg")
    .attr("viewBox", `0 0 ${width} ${height}`)
    .attr("width", width)
    .attr("height", height);
  
  const boxSize = (width - 2 * margin) / 2;
  
  // Title
  svg.append("text")
    .attr("x", width / 2)
    .attr("y", 50)
    .attr("text-anchor", "middle")
    .attr("font-size", "35px")
    .text("Predicted Class");
  
  // Predicted labels (top)
  svg.append("text")
    .attr("x", margin + boxSize / 2)
    .attr("y", 110)
    .attr("text-anchor", "middle")
    .attr("font-size", "30px")
    .html("P&#770;");
  
  svg.append("text")
    .attr("x", margin + boxSize * 1.5)
    .attr("y", 110)
    .attr("text-anchor", "middle")
    .attr("font-size", "30px")
    .html("N&#770;");
  
  // Actual Class label (left, rotated)
  svg.append("text")
    .attr("x", -height / 2)
    .attr("y", 35)
    .attr("text-anchor", "middle")
    .attr("font-size", "35px")
    .attr("transform", `rotate(-90)`)
    .text("Actual Class");
  
  // Actual labels (left)
  svg.append("text")
    .attr("x", 85)
    .attr("y", margin + boxSize / 2 + 10)
    .attr("text-anchor", "middle")
    .attr("font-size", "30px")
    .text("P");
  
  svg.append("text")
    .attr("x", 85)
    .attr("y", margin + boxSize * 1.5 + 10)
    .attr("text-anchor", "middle")
    .attr("font-size", "30px")
    .text("N");
  
  // Boxes
  const boxes = [
    { x: 0, y: 0, label: ["True", "Positive", "(TP)"] },
    { x: 1, y: 0, label: ["False", "Negative", "(FN)"] },
    { x: 0, y: 1, label: ["False", "Positive", "(FP)"] },
    { x: 1, y: 1, label: ["True", "Negative", "(TN)"] }
  ];
  
  boxes.forEach(box => {
    const g = svg.append("g");
    
    // Rectangle
    g.append("rect")
      .attr("x", margin + box.x * boxSize)
      .attr("y", margin + box.y * boxSize)
      .attr("width", boxSize)
      .attr("height", boxSize)
      .attr("fill", "none")
      .attr("stroke", "gray")
      .attr("stroke-width", 2);
    
    // Text
    const textX = margin + box.x * boxSize + boxSize / 2;
    const baseY = margin + box.y * boxSize + boxSize / 2 - 30;
    
    box.label.forEach((line, i) => {
      g.append("text")
        .attr("x", textX)
        .attr("y", baseY + i * 40)
        .attr("text-anchor", "middle")
        .attr("font-size", "30px")
        .text(line);
    });
  });
  
  return svg.node();
}

Figure 26.3: The Confusion Matrix

It’s evident from Figure 26.3 above that \begin{aligned} P &= TP + FN\\ N &= FP + TN\\ \hat P &=TP + FP\\ \hat N &=TN + FN. \end{aligned}

Accuracy

The accuracy measures the rate of the correct classification: acc = \frac{TP+TN}{TP+TN+FP+FN} \tag{26.3}

For imbalanced data, it’s recommended to class-specific precision as a more robust performance metric for a classifier.

Precision

The precision of a class measures the rate of the correct classification among labels classified as the class: p_{\tt 1} = \frac{TP}{TP+FP}\text{ and } p_{\tt 0} = \frac{TN}{TN+FN}. \tag{26.4}

Recall

The recall of a class measures the rate of the correct classification among true labels in that class: r_{\tt 1} = \frac{TP}{TP+FN}\text{ and } r_{\tt 0} = \frac{TN}{TN+FP} \tag{26.5}

The F1 score of the positive and negative classes are defined, respectively, as follows: f_{\tt 1} = \frac{2p_{\tt 1}r_{\tt 1}}{p_{\tt 1}+r_{\tt 1}}\text{ and } f_{\tt 0} = \frac{2p_{\tt 0}r_{\tt 0}}{p_{\tt 0}+r_{\tt 0}}. \tag{26.6}

Confusion Matrix

Compute the accuracy of a model that renders the following confusion matrix: \begin{bmatrix} 22 & 10 \\ 5 & 25 \end{bmatrix}.

\bold{y}=\frac{1}{d}(\bold{z}-c\bold{x})\bold{y}=\frac{1}{d}(\bold{z}+c\bold{x})\bold{y}=\frac{\bold{z}-c\bold{x}}{d}Not always possible

Possible only when d\neq0. In that case, we can write \bold{y}=\frac{1}{d}(\bold{z}-c\bold{x}).

An Example

Population

viewof w0 = Inputs.range([-5, 5], {value: 0, step: 0.1, label: tex`w_0`})
viewof w1 = Inputs.range([-5, 5], {value: 0, step: 0.1, label: tex`w_1`})

rnd = d3.randomUniform(-10, 10);
D = d3.range(N).map(() => {
      const x = rnd()
      const y = d3.randomBernoulli(sigmoid(w0+w1 * x))();
      return {x: x, y: y, yhat: sigmoid(w0_opt+w1_opt * x) >= 0.5 ? 1 : 0} 
});

viewof N = Inputs.range([0, 100], {value: 20, step: 1, label: tex`N`})
Plot.plot({
  grid: true,
  marks: [
    Plot.dot(D, {
      x: "x", 
      y: "y",
      fill: "y"
    })
  ]
})

L = function(D, w0, w1) {
  return D.reduce( (res, e) =>
    res - [e.y * Math.log(sigmoid(w0+w1*e.x)) + (1-e.y) * Math.log(1-sigmoid(w0+w1*e.x))], 0
  ) / D.length;
}
L(D, w0, w1);

Plotly = require("https://cdn.plot.ly/plotly-2.27.0.min.js")
a = {
  const n = 50;
  return d3.range(-10, 10, 10/n);
}

b = {
  const n = 50;
  return d3.range(-10, 10, 10/n);
}

surfaceData = {
  const z = [];
  for (let i = 0; i < b.length; i++) {
    const row = [];
    for (let j = 0; j < a.length; j++) {
      row.push(L(D, a[j], b[i]));
    }
    z.push(row);
  }
  
  return [{
    type: 'surface',
    x: a,
    y: b,
    z: z,
    colorscale: 'Viridis',
    contours: {
      z: {
        show: true,
        usecolormap: true,
        highlightcolor: "limegreen",
        project: { z: true }
      }
    }
  }];
}

// Create the plot
{
  const div = html`<div style="width: 700px; height: 600px;"></div>`;
  
  Plotly.newPlot(div, surfaceData, {
    title: 'Cross-entropy',
    scene: {
      xaxis: { title: "w_0" },
      yaxis: { title: "w_1" },
      zaxis: { title: "L" },
      camera: {
        eye: { x: 1.5, y: 1.5, z: 1.3 }
      },
    annotations: [{
        x: 0,
        y: 0,
        z: 0,
        text: "Minimum: {(min_a, min_b, min_z)}",
        showarrow: true,
        arrowhead: 2,
        arrowsize: 1,
        arrowwidth: 2,
        arrowcolor: 'red',
        ax: 40,
        ay: -40,
        font: {
          size: 14,
          color: 'red'
        }
      }]
    },
    width: "100%",
    height: 700
  });
  
  return div;
}

Your Classifier

viewof w0_opt = Inputs.range([-5, 5], {value: 0, step: 0.1, label: tex`w_0^*`})
viewof w1_opt = Inputs.range([-5, 5], {value: 0, step: 0.1, label: tex`w_1^*`})