Conditional Probabilities
Conditional Probability
Suppose A and B are events.
Conditional probability is the likelihood of an event occurring given that we know another event has occurred.
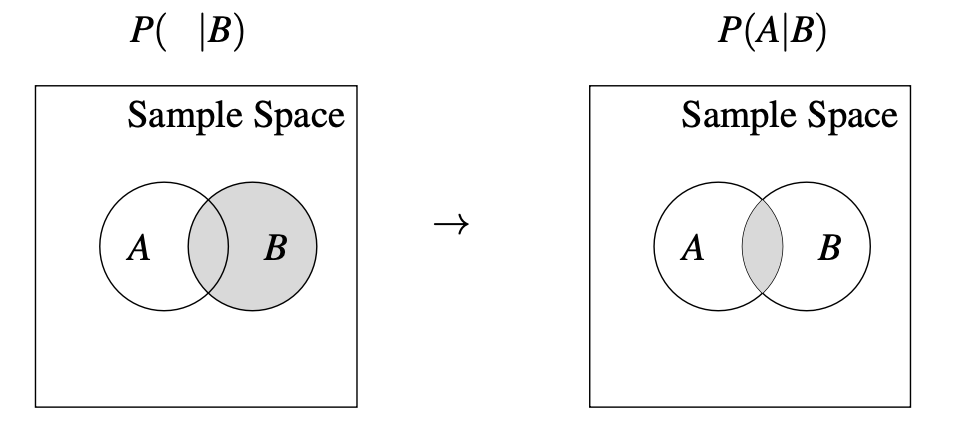
P(A|B) = \frac{P(A \cap B)}{P(B)}
Notice that the conditioned event becomes the new sample space.
If P(B) \neq 0, then the probability of the intersection normalized by the conditioned space. Else P(B) = 0, then P(A|B) is undefined.
Product Rule
Suppose A and B are events.
The product rule states that the probability of two events A and B occurring together A \cap B is given by the probability of one event occurring given the other P(A|B) or P(B|A) multiplied by the probability of the other event.
P(A \cap B) = P(A|B) P(B) = P(B|A) P(A)
Total Probability Theorem
Suppose A_{1,...,n} and B are events.
The total probability theorem allows us to compute the likelihood of an event by summing over conditional probabilities of different partitions of the sample space.
P(B) = P(B|A_1) P(A_1) + P(B|A_2) P(A_2) + P(B|A_3) P(A_3)

In general terms:
P(B) = P(B|A_1) P(A_1) + ... + P(B|A_n) P(A_n)
Experiment: Classifying emails as spam S or not spam NS based on the word W or not the word NW “free”.
P(S) = 0.4
P(NS) = 0.6
P(W|S) = 0.7
P(W|NS) = 0.1
Find the probability of P(S|W):
P(S|W) = \frac{P(S \cap W)}{P(W)} = \underbrace{\frac{P(W|S)P(S)}{P(W|S)P(S) + P(W|NS)P(NS)}}_{Bayes' \ Theorem} = \frac{0.7 * 0.4}{0.7 * 0.4 + 0.1 * 0.6} = 0.82