Probabilities

A formal framework that defines probability using three fundamental rules, ensuring consistency in measuring uncertainty. 🎲

Methodology

Steps to perform a probabilistic model:

  1. Specify sample space.
  2. Define probability law (must align with probability axioms).
  3. Identify event of interest.
  4. Calculate…

Sample Space

A sample space is a set of all possible outcomes from an experiment.

Sample \ Space = \{\text{Heads}, \text{Tails}\}

An experiment is any procedure that can be repeated and has a well-defined set of outcomes.

\text{Flipping a fair coin}

An outcome is the end result of an experiment, or an element in the sample space.

\text{Heads}

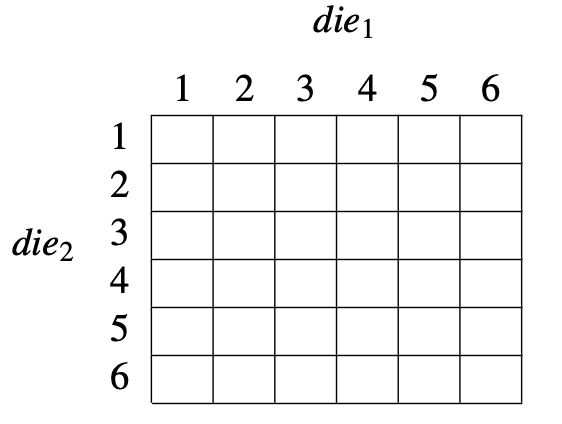
Illustration: Discrete Sample Space

Experiment: Rolling two fair die at the same time.

Sample \ Space = \{ (x, y) : x,y \in \mathbb{N}, 1 \leq x, y \leq 6 \}

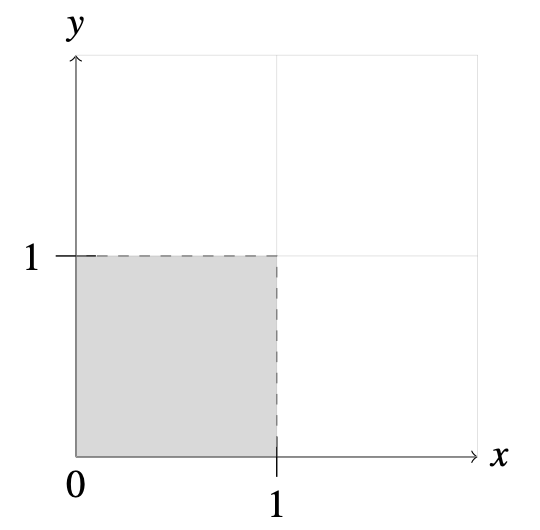
Illustration: Continuous Sample Space

Experiment: Measure two continuous variables in the range [0,1]

Sample\ Space = \{ (x, y) : x,y \in \mathbb{R}, 0 \leq x, y \leq 1 \}

Events and Experiment

An event is a subset of the sample space.

Events are important because they ultimately get assigned probabilities.

Experiment: Rolling a die once.

Sample \ Space = \{1,2,3,4,5,6\}

What is the event of rolling a 1?

\{1\} \subseteq \{1,2,3,4,5,6\}

What is the event of rolling an odd number?

\{1, 3, 5\} \subseteq \{1,2,3,4,5,6\}

Probability Axioms and Probability Law

Suppose A and B are events.

Kolmogorov probability axioms are the foundations of axiomatic probability theory:

  1. Nonnegativity: P(Event) \geq 0
  2. Normalization: P(Sample\ Space) = 1
  3. Additivity: If A \cap B = \emptyset, P(A \cup B) = P(A) + P(B)

Probability laws are additional axioms mathematically derived from Kolmogorov probability axioms.

Exercise

Experiment: Rolling two fair die at the same time.

Let all outcomes be equally likely.

P(A) = \frac{|A|}{|Sample\ Space|}

Find the following probabilities:

  1. P(die_1 = 1)
  2. P(\text{max}(die_1, die_2) = 2)
  1. P(die_1 = 1) = \frac{6}{36} \approx 0.1\bar{6}
  2. P(\text{max}(die_1, die_2) = 2) = \frac{2}{36} \approx 0.0\bar{5}
Exercise

Experiment: Measure two continuous variables in the range [0,1]

Sample\ Space = \{ (x, y) : x,y \in \mathbb{R}, 0 \leq x, y \leq 1 \}

Find the following probabilities:

  1. P(x = 0.5 , y = 0.5)
  2. P(x+y \geq 1)
  1. P(x = 0.5 , y = 0.5) = 0
  2. P(x+y \geq 1) = 0.5