Discrete Random Variables
Discrete Random Variable
A discrete random variable is a mapping \(X\) of all of the outcomes of a sample space to numerical values \(x \in \mathbb{Z}\).
\[ X: Outcome \in Sample \ Space \to x \in \mathbb{Z} \]
Probability Mass Function (PMF)
A probability mass function (PMF) is a mapping of values \(x\) of discrete random variables \(X\) to probabilities \([0,1]\).
\[ p_{X}(x) = P(X = x) \]
PMF has properties: \[ p_{X}(x) \geq 0, \quad \sum_{x} p_{X}(x) = 1 \]
Cumulative Distribution Function (CDF)
The cumulative distribution function (CDF) for discrete random variables is defined as:
\[ F_{X}(x) = P(X \leq x) = \sum_{k \leq x} p_{X}(k) \]
Relation to PMF: \[ p_{X}(x) = \frac{dF_{X}(x)}{dx} \]
\[ F_{X}(x) = \sum_{k \leq x}p_{X}(k) \]
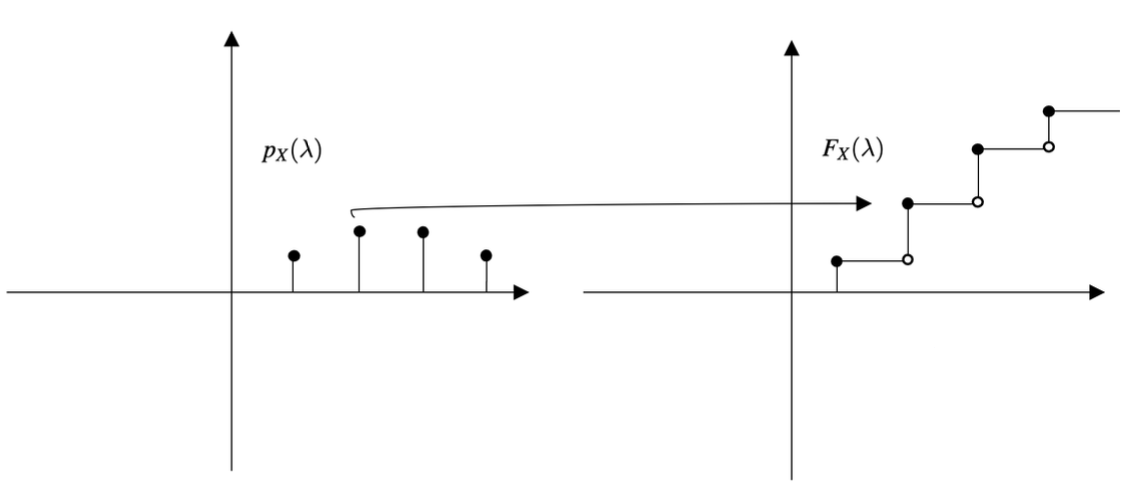
Illustration: PMF and CDF
Expectation and Variance of PMFs
Discrete expectation, or mean, is the average numerical value that the discrete random variable takes over the PMF. \[ E[X] = \sum_{x} x \ p_{X}(x) \]
Discrete variance is the expected squared difference from the mean of a PMF. \[ Var[X] = E[(X - E[X])^{2}] = \sum_{x}(x - E[X])^2 p_{X}(x) \]
Joint and Marginal PMFs
The joint PMF calculates the intersection of two discrete random variables: \[ p_{X,Y}(x_{1},x_{2}) = P(X = x_{1}, Y = x_{2}) \]
From the previous definition we can also compute the marginal PMF for a particular random variable: \[ p_{X}(x_{1}) = \sum_{x_{2}} p_{X,Y}(X = x_{1},Y = x_{2}) \]
Conditional Expectation of PMFs
The conditional PMF gives the probability distribution of a discrete random variable given that another variable has a specific value. \[ p_{X|Y}(x_{1}| x_{2}) = \frac{p_{X,Y}(x_{1}, x_{2})}{p_{Y}(x_{2})} \]
The conditional expectation is the expected value of a discrete random variable given that another variable is fixed at a specific value. \[ E[X| Y = x_{2}] = \sum_{x_{1}} x_{1} \frac{p_{X,Y}(x_{1}, x_{2})}{p_{Y}(x_{2})} \]
Independence
Two discrete random variables are independent if:
\[ p_{X,Y}(x_{1}, x_{2}) = p_{X}(x_{1}) p_{Y}(x_{2}) \]
For multiple discrete random variables: \[ p_{X_{1},...,X_{n}}(x_{1}, ..., x_{n}) = p_{X_{1}}(x_{1}) ... \ p_{X_{n}}(x_{n}) \]