11.2 Advanced Monte Carlo Tree Search
Motivation
Problem
Require an algorithm that leverages neural networks for more efficient MCTS acting and updating.
Solution

Google DeepMind 2016
Link to Research Paper

Google DeepMind 2020
Link to Research Paper
Advanced MCTS: Illustration
- Policy Network: Guides expansion by prioritizing actions with high probabilities, reducing the search space:
\[ P(a|s) \propto \pi(a|s; \theta) \]
- Value Network: Replaces random rollouts with a learned estimate of the value function:
\[ Q(s,a) \approx V(s; \theta) \]
Advanced MCTS: Steps
Selecting:
\[ A_t = \arg\max_a \left[ Q(s, a) + C \cdot \pi(a | s; \theta) \frac{\sqrt{\sum_b N(s, b)}}{1 + N(s, a)} \right] \]Expanding:
If the selected node has unvisited children, expand.Simulating:
\[ V(s; \theta) = (1 - \lambda) V(s; \theta) + \lambda R \]Updating:
\[ N(s, a) = N(s, a) + 1 \]
\[ Q(s, a) = Q(s, a) + \frac{1}{N(s, a)} \left( V(s; \theta) - Q(s, a) \right) \]
Advanced MCTS: Results
Results of 5-game tournament against Fan Hui (Elo in 2016: 3036).
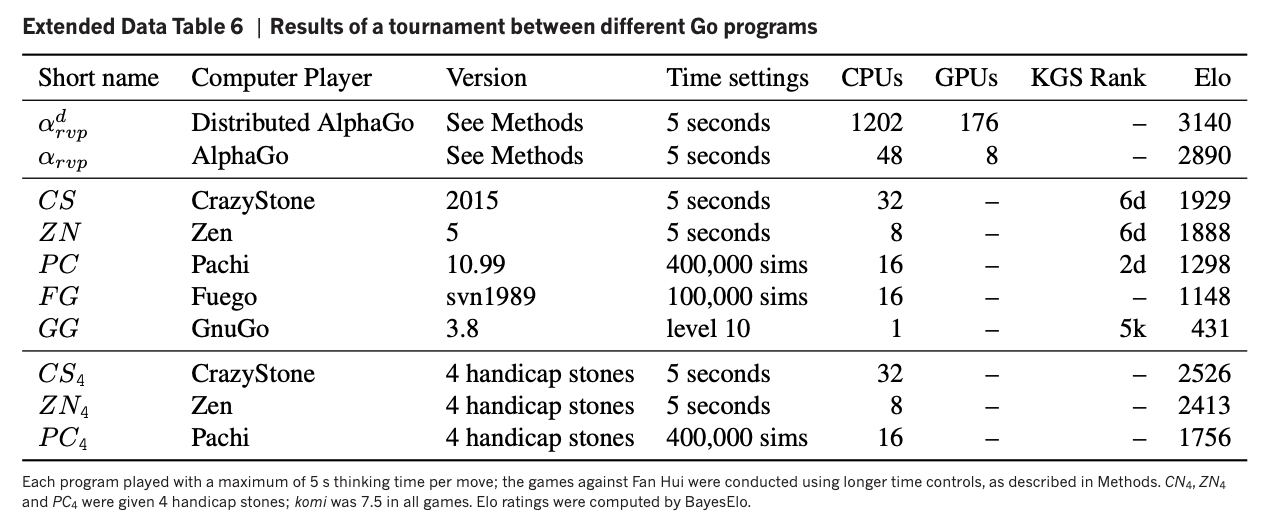
AlphaGo won all 5 games.
MuZero MCTS with Neural Networks
- Selecting:
\[ A_t = \arg\max_a \left[ Q(s,a) + C \frac{\pi(a|s)}{1 + N(s,a)} \right] \]
Using Prediction Network \(f(s)\) to compute \(\pi\) and \(Q\)
- Expanding:
Use Representation Network \(h(o)\) to create state
Prediction Network \(f(s)\) generates initial policy/value
- Simulating:
Dynamics Network \(g(s,a)\) predicts next state and reward
- Updating:
\[ N(s,a) = N(s,a) + 1 \]
\[ Q(s,a) = \frac{1}{N(s,a)} \sum_i V_i(s) \]
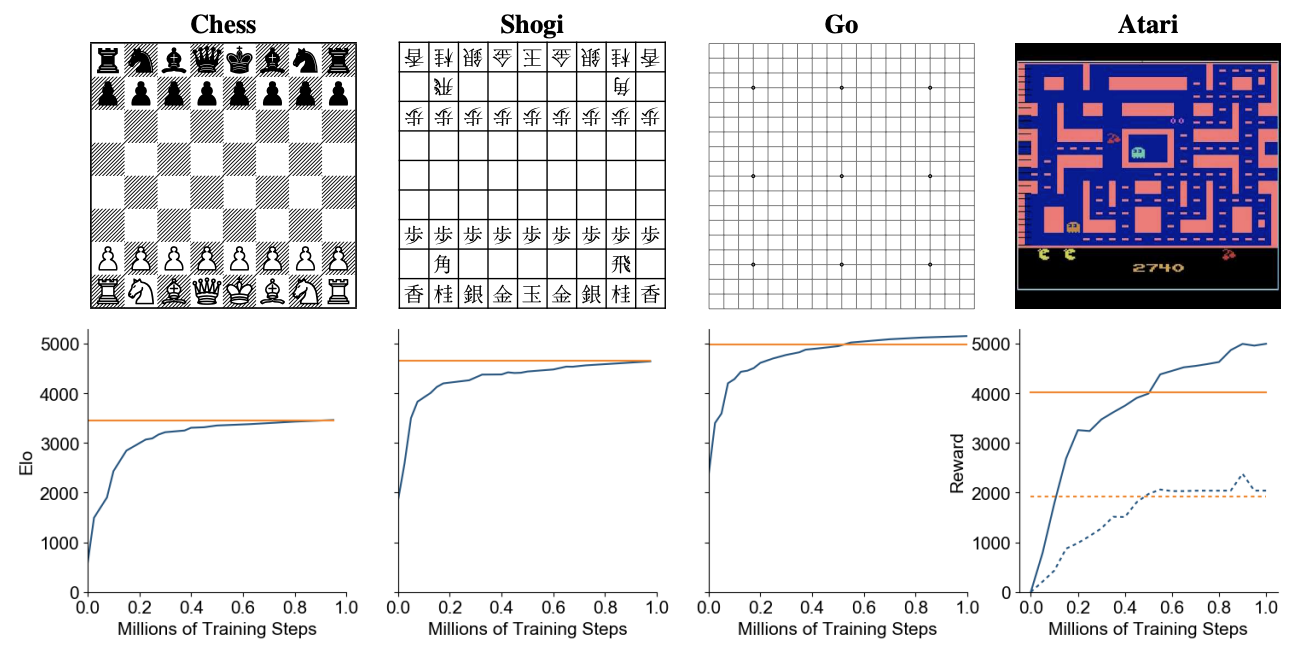
Advanced MCTS: AlphaZero Performance
Orange line indicates best result of AlphaZero (AlphaGo trained purely on self-play).