6.3 Q-Learning

A formal framework that defines probability using three fundamental rules, ensuring consistency in measuring uncertainty. 🎲

Q-Learning

TD off-policy method we can both update and estimate the optimal action-value function directly:

\[ Q(S_{t},A_{t}) = Q(S_{t},A_{t}) + \alpha [ R_{t+1} + \gamma \max_{a} Q(S_{t+1},a) - Q(S_{t},A_{t})] \]

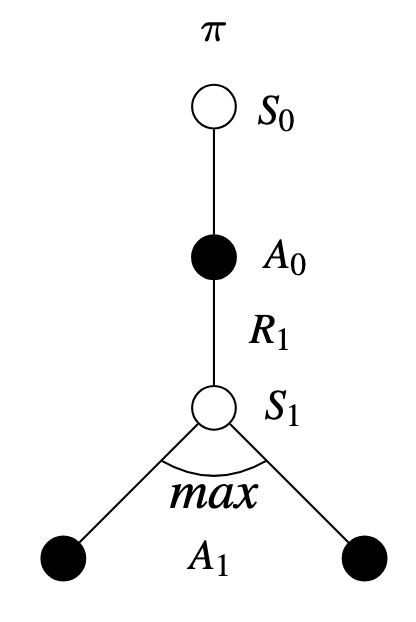
Q-Learning is a breakthrough in reinforcement learning due to its simplification of algorithm analysis and early convergence proofs.

Pseudocode

\begin{algorithm} \caption{TD Q-Learning} \begin{algorithmic} \State \textbf{Initialize:} \State $Q(s, a) \gets 0$ for all $(s, a) \in S \times A$ \State $\gamma \in [0, 1)$ \State $\alpha \in (0, 1]$ \State $\epsilon > 0$ \State $\pi \gets$ arbitrary $\epsilon$-soft policy \State \textbf{Loop for each episode:} \State Initialize $S_{0}$ \Repeat \State Choose $A_{t}$ from $S_{t}$ using $\pi$ \State Take action $A_{t}$, observe $R_{t+1}$ and $S_{t+1}$ \State $Q(S_{t}, A_{t}) \gets Q(S_{t}, A_{t}) + \alpha \left[R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a) - Q(S_{t}, A_{t})\right]$ \State $S_{t} \gets S_{t+1}$ \Until{$S_{t}$ is terminal} \end{algorithmic} \end{algorithm}