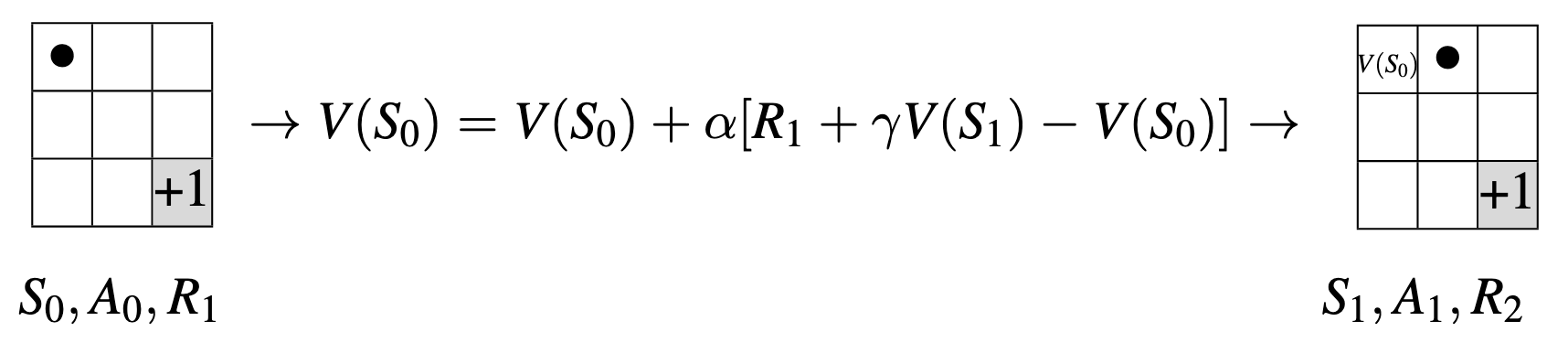6.1 Temporal Difference (TD) Prediction
TD Prediction
Temporal Difference (TD) is a learning rule that is a combination of Monte Carlo and Dynamic Programming ideas.
- TD methods, like Monte Carlo, learn from experience by updating estimates of nonterminal states along a trajectory \(\pi\).
- TD methods, like Dynamic Programming, update based on an existing estimate \(V(S_{t+1})\).
TD methods at time \(t + 1\) immediately form a target and make a useful update using the observed reward \(R_{t+1}\) and the estimate \(V_(S_{t+1})\) in a incremental fashion:
\[ V(S_{t}) = V(S_{t}) + \underbrace{\alpha}_{Step \ Size} [ \underbrace{\underbrace{R_{t+1} + \gamma V(S_{t+1})}_{Target \ Update} - V(S_{t})}_{TD \ Error}] \]
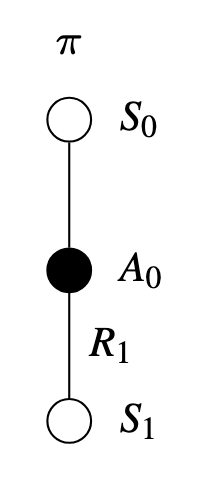
Pseudocode
\begin{algorithm} \caption{TD Prediction} \begin{algorithmic} \State \textbf{Initialize:} \State $V(s) \gets 0$ for all $s \in S$ \State $\gamma \in [0, 1)$ \State $\alpha \in (0, 1]$ \State \textbf{Loop for each episode:} \State Initialize $S_{0}$ \Repeat \State $A_{t} \gets$ action given by $\pi$ for $S_{t}$ \State Take action $A_{t}$, observe $R_{t+1}$ and $S_{t+1}$ \State $V(S_{t}) \gets V(S_{t}) + \alpha \left[R_{t+1} + \gamma V(S_{t+1}) - V(S_{t})\right]$ \State $S_{t} \gets S_{t+1}$ \Until{$S_{t}$ is terminal} \end{algorithmic} \end{algorithm}
Environment GridWorld
Assume \(\gamma = 0.9\)
Suppose we follow the trajectory of \(\pi\) for one episode: