2.3 Conditioning
Conditional Probability
Suppose \(A\) and \(B\) are events.
Conditional probability is the likelihood of an event occurring given that we know another event has occurred.
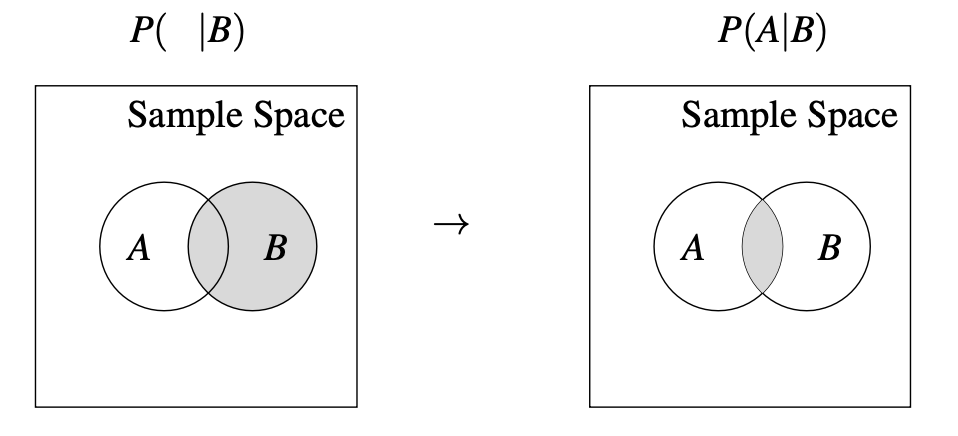
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
Notice that the conditioned event becomes the new sample space.
If \(P(B) \neq 0\), then the probability of the intersection normalized by the conditioned space. Else \(P(B) = 0\), then \(P(A|B)\) is undefined.
Product Rule
Suppose \(A\) and \(B\) are events.
The product rule states that the probability of two events \(A\) and \(B\) occurring together \(A \cap B\) is given by the probability of one event occurring given the other \(P(A|B)\) or \(P(B|A)\) multiplied by the probability of the other event.
\[ P(A \cap B) = P(A|B) P(B) = P(B|A) P(A) \]
Total Probability Theorem
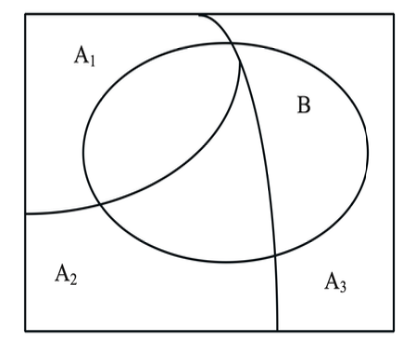
Suppose \(A_{1,...,n}\) and \(B\) are events.
The total probability theorem allows us to compute the likelihood of an event by summing over conditional probabilities of different partitions of the sample space.
\[ P(B) = P(B|A_1) P(A_1) + P(B|A_2) P(A_2) + P(B|A_3) P(A_3) \]
In general terms:
\[ P(B) = P(B|A_1) P(A_1) + ... + P(B|A_n) P(A_n) \]
Experiment: Classifying emails as spam \(S\) or not spam \(NS\) based on the word \(W\) or not the word \(NW\) “free”.
\[ P(S) = 0.4 \]
\[ P(NS) = 0.6 \]
\[ P(W|S) = 0.7 \]
\[ P(W|NS) = 0.1 \]
Find the probability of \(P(S|W)\):
\[ P(S|W) = \frac{P(S \cap W)}{P(W)} = \underbrace{\frac{P(W|S)P(S)}{P(W|S)P(S) + P(W|NS)P(NS)}}_{Bayes' \ Theorem} = \frac{0.7 * 0.4}{0.7 * 0.4 + 0.1 * 0.6} = 0.82 \]