6.2 SARSA
SARSA
TD on-policy method we must estimate \(q_{\pi}(s, a)\) for the current behavior policy \(\pi\) and for all states \(s \in S\) and actions \(a \in A(S)\)
The theorems assuring the convergence of state values under TD Prediction also apply to the corresponding algorithm for action values: \[ Q(S_{t},A_{t}) = Q(S_{t},A_{t}) + \alpha [ R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_{t},A_{t})] \]
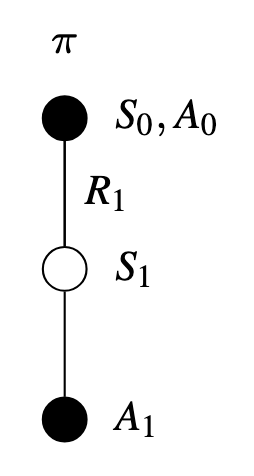
This rule uses every element of the quintuple of events (\(S_{t}, A_{t}, R_{t+1}, S_{t+1}, A_{t+1}\))
Pseudocode
\begin{algorithm} \caption{TD SARSA} \begin{algorithmic} \State \textbf{Initialize:} \State $Q(s, a) \gets 0$ for all $(s, a) \in S \times A$ \State $\gamma \in [0, 1)$ \State $\alpha \in (0, 1]$ \State $\epsilon > 0$ \State $\pi \gets$ arbitrary $\epsilon$-soft policy \State \textbf{Loop for each episode:} \State Initialize $S_{0}$ \State Choose $A_{0}$ from $S_{0}$ using $\pi$ \Repeat \State Take action $A_{t}$, observe $R_{t+1}$ and $S_{t+1}$ \State Choose $A_{t+1}$ from $S_{t+1}$ using $\pi$ \State $Q(S_{t}, A_{t}) \gets Q(S_{t}, A_{t}) + \alpha \left[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_{t}, A_{t})\right]$ \State $S_{t} \gets S_{t+1}$ \State $A_{t} \gets A_{t+1}$ \Until{$S_{t}$ is terminal} \end{algorithmic} \end{algorithm}