Recommendation Systems

Application: Recommendations Systems 💡

NoteFairfax County Public Schools (FCPS) Recommendation Systems

Fairfax County Public Schools (FCPS) sales.csv and production.csv preprocessed data enables us to construct recommendation systems leveraging Contextual Multi-Armed Bandits (CMAB).

Health-Aware School Meal Recommendations (Capstone Group 8)

Using FCPS sales.csv:

Suppose that our action space \(\mathcal{A}\) is composed of our menu items being served:

\[ \mathcal{A} \gets \{ \text{Cereal} , ... , \text{Bagels} \} \]

For a particular date \(t\), we restrict our selection of menu items to only those that were actually served (mask):

\[ \mathcal{A}_{t} \gets \{ \text{Cereal} , \text{Apples} , \text{Juice} \} \]

For each available item \(a \in \mathcal{A}_t\), we construct feature vectors \(\mathbf{x}_{t,a}\) that include nutritional, popularity and school related information:

\[ \mathbf{x}_{t,a} = \begin{bmatrix} p \in \mathbb{R} \gets \text{protein grams (one serving)} \\ c \in \mathbb{R} \gets \text{carbohydrate grams (one serving)} \\ f_a \in \mathbb{R} \gets \text{fats grams (one serving)} \\ f_i \in \mathbb{R} \gets \text{fiber grams (one serving)} \\ s \in \mathbb{R} \gets \text{sugar grams (one serving)} \\ h \in \mathbb{N} \gets \text{historical sales count} \\ g \gets \text{grade level} \\ d \gets \text{day of week} \\ \vdots \end{bmatrix} \]

We then compute the parameter estimates \(\hat{\boldsymbol{\theta}}_a\) and evaluate the scores \(\mathbf{p}_{t,a}\). The action is selected according to

\[ R_t = \text{total sales count} + \lambda \ \text{health score} \]

where \(\lambda\) is a penalization factor that controls the trade-off between popularity (sales) and nutritional quality (health). A higher \(\lambda\) places greater emphasis on nutritional value, while a lower \(\lambda\) prioritizes maximizing sales volume.

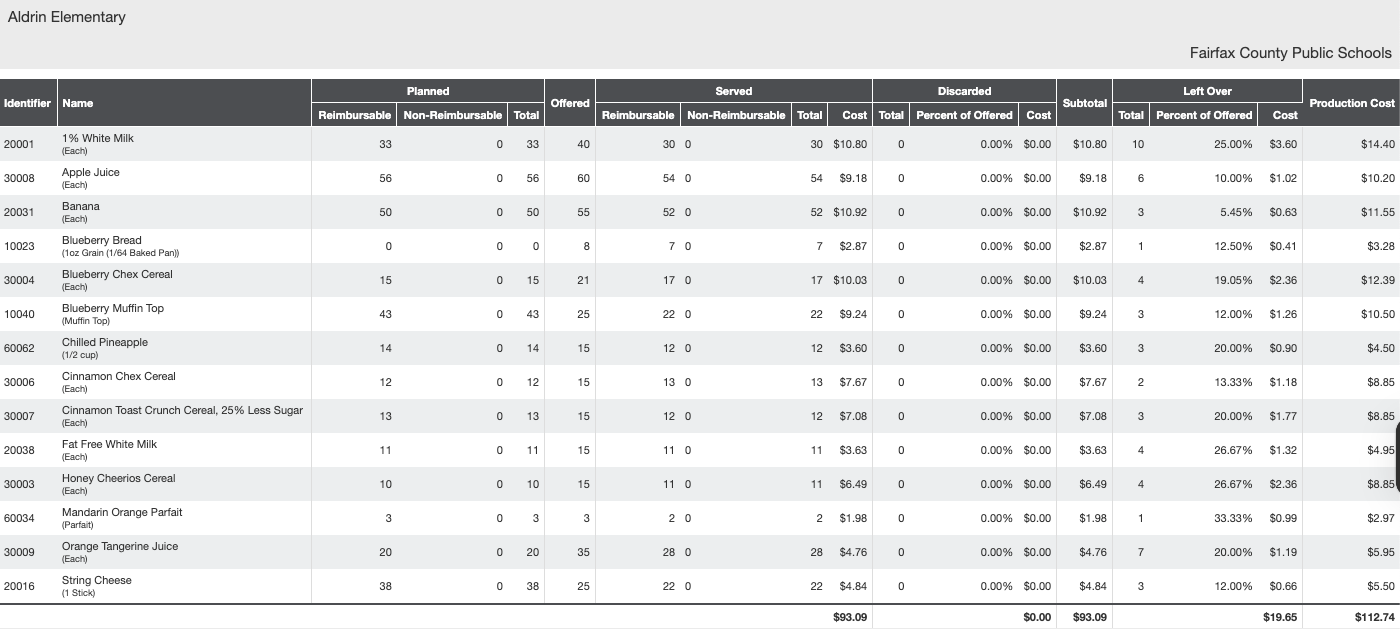
Waste Minimization Recommendations (Capstone Group 1)

Using FCPS production.csv:

Suppose that our action space \(\mathcal{A}\) is composed of our menu items being served:

\[ \mathcal{A} \gets \{ \text{Cereal} , ... , \text{Bagels} \} \]

For a particular date \(t\), we restrict our selection of menu items to only those that were actually served (mask):

\[ \mathcal{A}_{t} \gets \{ \text{Cereal} , \text{Apples} , \text{Juice} \} \]

For each available item \(a \in \mathcal{A}_t\), we construct feature vectors \(\mathbf{x}_{t,a}\) that include nutritional factors and contextual information:

\[ \mathbf{x}_{t,a} = \begin{bmatrix} l \in \mathbb{N} \gets \text{Historical Leftover} \\ s \in \mathbb{N} \gets \text{Historical Served Count} \\ g \gets \text{grade level} \\ d \gets \text{day of week} \\ \vdots \end{bmatrix} \]

We then compute the parameter estimates \(\hat{\boldsymbol{\theta}}_a\) and evaluate the scores \(\mathbf{p}_{t,a}\). The action is selected according to the negative discarded cost:

\[ R_t = - (\text{Left Over Cost} + \text{Discarded Cost}) \]

where the bandit aims to minimize waste. A higher (less negative) reward corresponds to items with lower discarded cost, guiding the algorithm to favor menu items that are both consumed and cost-efficient.

NoteGoogle RecSim

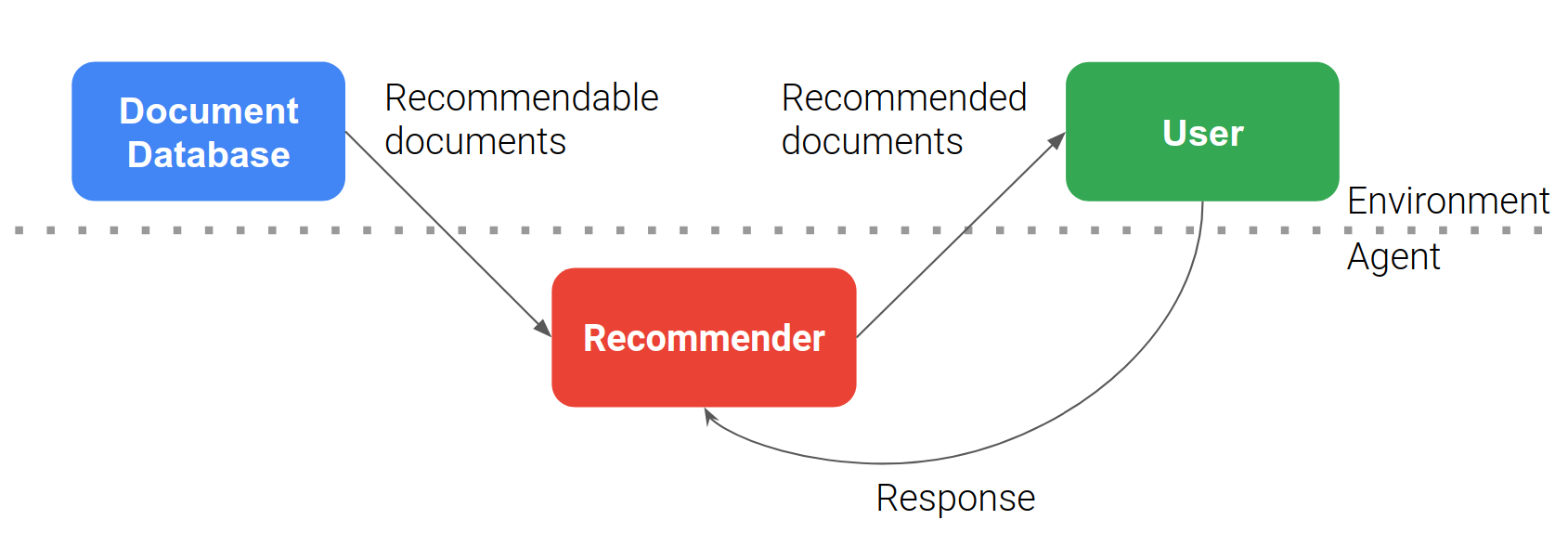
As seen in lecture 1, Google provides configurable recommendation system using OpenAI Gymnasium.


Google Research 2019 (Ie et al. 2019)
Link to Research Paper

To install recsim simply just run the following pip command:

pip install recsim

main.py should run as follows:

environment.py should contain the following:

Adaptation to User Preference Drift (Capstone Group 12 & Greedy Policy Crew 💰)

Demo of how to run recsim by Google.

Environment (Capstone Group 12)

Demo of how to create a enviornment by Google.

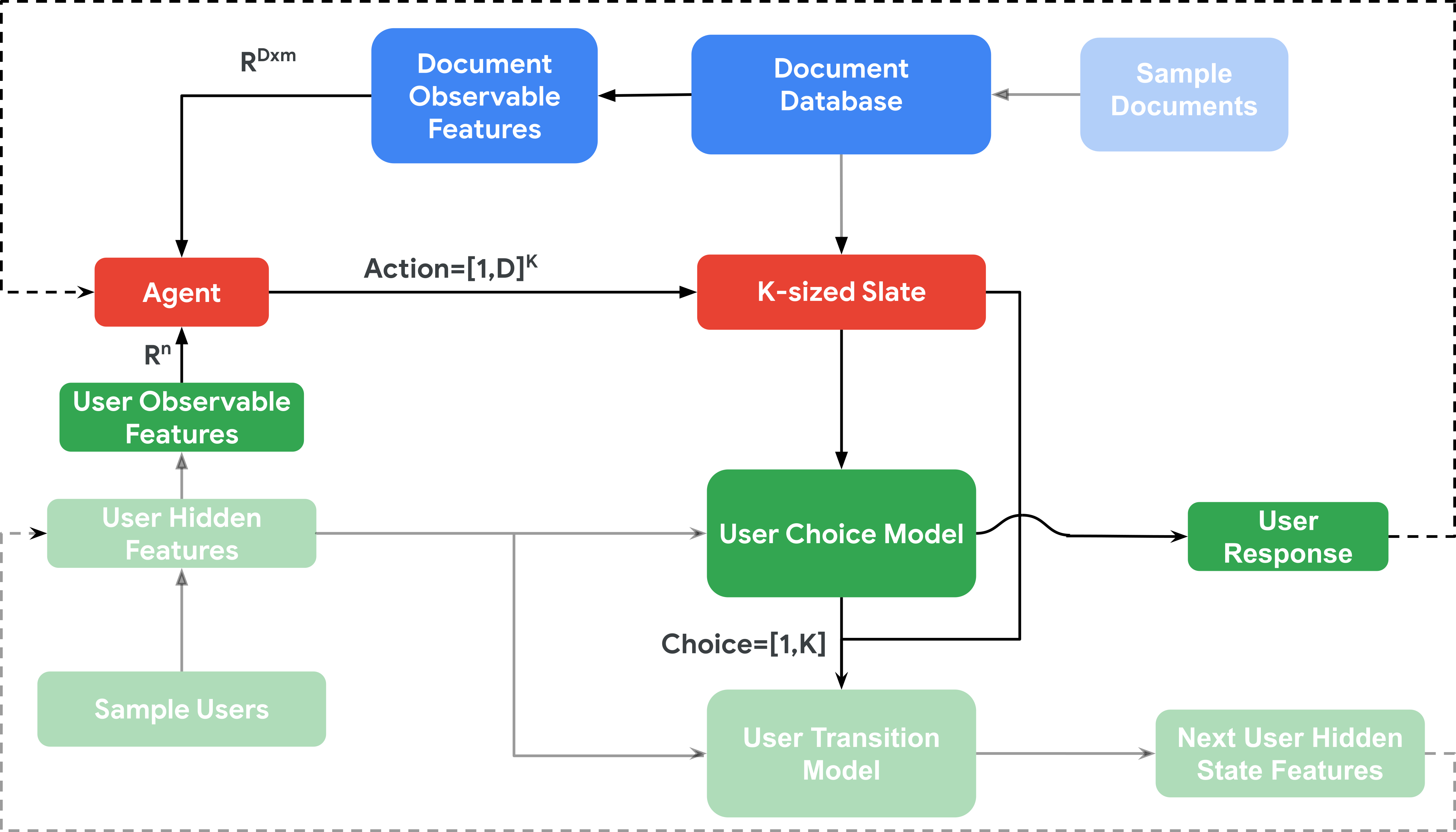
Environment Document Database

  • DriftingDocument (subclass of recsim.document.AbstractDocument)
    This class would hold documents \(d_i\) with features: \(\mathbf{x}\) topic, \(p\) popularity score, and \(q\) quality score.

\[ d_i = \Big( \mathbf{x}_i, \; p_i, \; q_i \Big) \]

  • DriftingDocumentSampler (subclass of recsim.document.AbstractDocumentSampler)
    This class would generate documents at each time step by sampling their features \(\Big( \mathbf{x}, \; p, \; q \Big)\) from a distribution.

\[ \mathcal{D}_t = \{ d_1, d_2, \dots, d_{N_t} \}, \quad d_i \sim P_D(\mathbf{x}, p, q) \]

Environment User

  • DriftingUserState (subclass of recsim.user.AbstractUserState)
    This class would store for a particular user \(\ u_j \ \) at time \(\ t\): \(\boldsymbol{\theta}_{j,t}\) latent preference vector, \(\sigma_{j,t}\) user satisfaction or engagement score, \(\phi_{j,t}\) fatigue variable, and \(\tau_{j,t}\) current timestep.

\[ u_{j,t} = (\boldsymbol{\theta}_{j,t}, \; \sigma_{j,t}, \; \phi_{j,t}, \; \tau_{j,t}) \]

  • DriftingUserSampler (subclass of recsim.user.AbstractUserSampler)
    This class would generate a population of users \(\mathcal{U}_0\) at time \(t=0\):

\[ \mathcal{U}_0 = \{ u_{1,0}, u_{2,0}, \dots, u_{M,0} \}, \quad u_{j,0} \sim P_U(\boldsymbol{\theta}, \sigma, \phi) \]

  • DriftingResponseModel (subclass of recsim.user.AbstractResponseModel)
    This class would define how a user reacts to a document, mapping (user state, document features) into probabilities of click.

\[ \Pr(\text{click}_{j,i,t} = 1) = \sigma \Big( \boldsymbol{\theta}_{j,t}^\top \mathbf{x}_i + \beta_1 q_i + \beta_2 p_i + \epsilon_{j,i,t} \Big) \]

  • DriftingUserModel (subclass of recsim.user.AbstractUserModel)
    This class would coordinate the simulation: advancing the user state, calling the response model, and updating preferences via a drift process.

\[ \boldsymbol{\theta}_{j,t+1} = (1-\alpha)\boldsymbol{\theta}_{j,t} + \alpha \mathbf{x}_{i,t} + \boldsymbol{\epsilon}_{j,t} \]