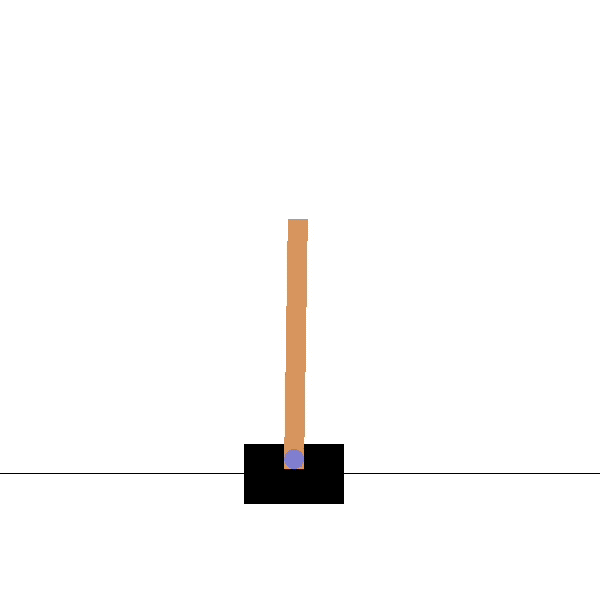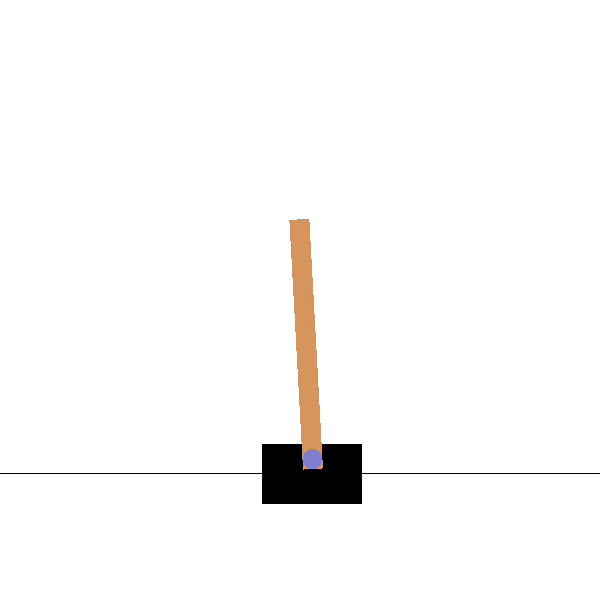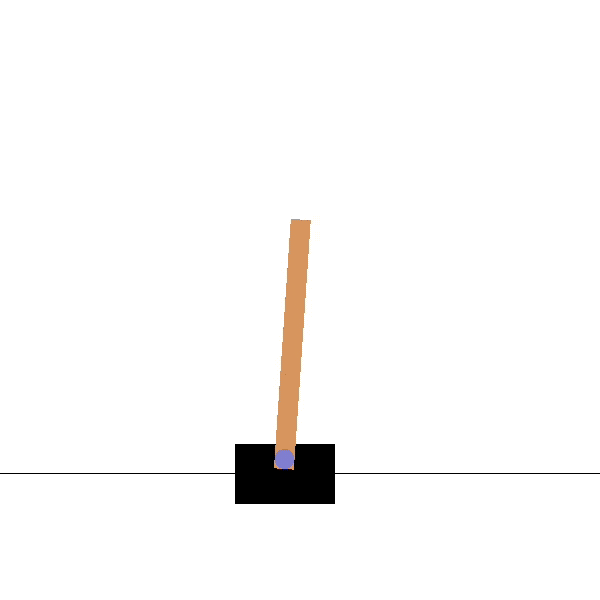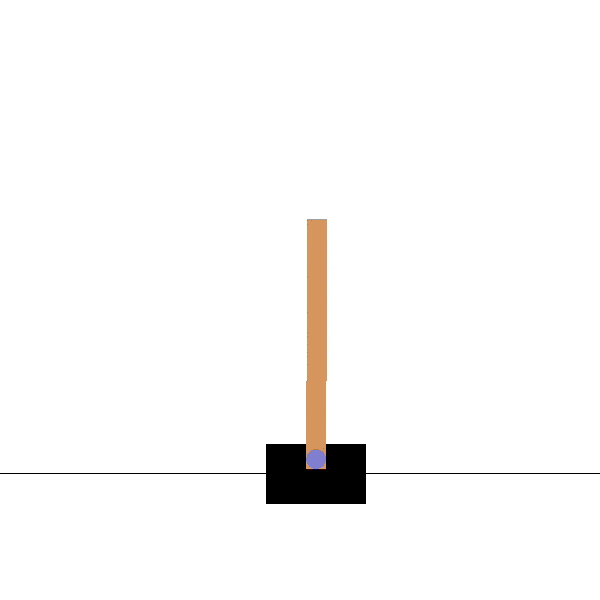9.2 Addressing Sparse Rewards
Before we can apply policy gradient methods effectively, we first need to solve the problem of high variance in the reward estimate:
\[ \hat{g} = \frac{1}{m} \sum^{m}_{i = 1} R(\tau^{i}) \sum^{T-1}_{t=0} \text{log} \nabla_\theta \pi(A_{t}|S_{t}, \theta) \]
How can we learn effective policies when reward signals are sparse and only received at the end of long trajectories?
Consider the following CartPole environment (Barto, Sutton, and Anderson 1983):
The state information \(\mathbf{s}\) is now the following vector:
\[ \mathbf{s} = \begin{bmatrix} cp \in (-4.8,4.8) \gets \text{Cart Position} \\ cv \in (-\inf,\inf) \gets \text{Cart Velocity} \\ pa \in (\approx -0.418 \ \text{rad}(-24°),\approx 0.418 \ \text{rad}(-24°)) \gets \text{Pole Angle} \\ pav_t \in (-\inf,\inf) \gets \text{Pole Angular Velocity} \\ \end{bmatrix} \]
The environment has a discrete action space \(\mathcal{A}\):
\[ \mathcal{A} = \{0 \gets \text{Push cart to the left}, 1 \gets \text{Push cart to the right}\} \]
The environment’s state transition dynamics \(P(s’, r \mid s, a)\) are calculated using classical mechanics and Euler Method:
\[ \begin{align} g &= 9.8 \quad \gets \text{gravity} \\ m &= 0.1 \quad \gets \text{pole mass} \\ M &= 1.0 \quad \gets \text{cart mass} \\ l &= 0.5 \quad \gets \text{half pole length} \\ \tau &= 0.02 \quad \gets \text{time step} \\ \end{align} \]
Angular Acceleration:
\[ \ddot{pa_t} = \frac{ g \sin(pa_t) + \cos(pa_t) \left(-\text{action} - m \cdot l \cdot pav_t^2 \sin(pa_t)\right)/(M + m) }{ l \left(\frac{4}{3} - \frac{m \cos^2(pa_t)}{M + m} \right) } \]
Cart acceleration:
\[ \ddot{cv_t} = \frac{ \text{action} + m \cdot l \left(pav_t^2 \sin(pa_t) - \ddot{p}_a \cos(pa_t)\right) }{M + m} \]
Euler integration:
\[ \begin{align} cp_{t+1} &= cp_t + \tau \cdot cv_t \\ cv_{t+1} &= cv_t + \tau \cdot \ddot{cv_t} \\ pa_{t+1} &= pa_t + \tau \cdot pav_t \\ pav_{t+1} &= pav_t + \tau \cdot \ddot{pa_t} \end{align} \]
Default Reward Function:
Since the goal is to keep the pole upright for as long as possible, by default, a reward of \(+1\) is given for every step taken, including the termination step. The default reward threshold is \(500\) for v1 and \(200\) for v0 due to the time limit on the environment.
Sparse Rewards:
If sutton_barto_reward=True, then a reward of \(0\) is awarded for every non-terminating step and \(-1\) for the terminating step. As a result, the reward threshold is \(0\) for v0 and v1.
The episode ends \(d\) (dones) if either of the following happens:
- Termination: Pole Angle is greater than \(\pm12°\).
- Termination: Cart Position is greater than \(\pm2.4\) (center of the cart reaches the edge of the display).
- Truncation: Episode length is greater than \(500\) (\(200\) for
v0).