6.2 SARSA

What if your learning came from walking the path you’re already on — mistakes and all? 🚶‍♂️

To move from prediction to control, we must estimate the action-value function \(q_{\pi}(s, a)\) for the current behavior policy \(\pi\) — and ensure we update it for all state-action pairs \((s, a)\) encountered during interaction with the environment.

WarningProblem

How can we leverage the Temporal Difference learning rule to approximate the optimal policy \(\approx \pi_{*}\) — while still exploring, ensuring every state-action \((s,a)\) pair is visited, and updating only from actions actually taken by the current policy \(\pi\)?

NoteReal Life Example 🧠

Suppose you’re using a music recommendation app:

  • \(S\) — Your current mood or environment (e.g., studying, running, relaxing).
  • \(A\) — The app suggests a song based on your current preferences.
  • \(R\) — You either enjoy the song, skip it, or dislike it — giving implicit feedback.
  • \(S', A'\) — The next song plays, and you make another decision.

State \(S\): Feeling energetic. Action \(A\): Play Salsa (Oscar De León). Reward \(R\): Always enjoyable — positive feedback reinforces this choice. Next state \(S'\) and action \(A'\) follow after this song.

State \(S\): Feeling upbeat. Action \(A\): Play Reggaeton (Feid). Reward \(R\): Mostly hits, sometimes skipped — app updates preference based on this feedback.

State \(S\): Feeling calm. Action \(A\): Play Jazz. Reward \(R\): New genre, unknown feedback — exploration allows the app to learn preferences.

How can your music app learn what you like while still exploring new genres — using your actual listening behavior, one song at a time?

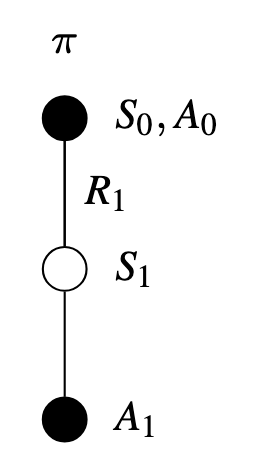
SARSA is an on-policy TD control method that updates action-value estimates based \(q_{\pi}(s, a)\) on the trajectory actually followed by the current policy \(\pi\) — including any exploration it performs.

\[ Q(S_{t},A_{t}) = Q(S_{t},A_{t}) + \alpha [ R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_{t},A_{t})] \]

This rule uses every element of the quintuple of events (\(S_{t}, A_{t}, R_{t+1}, S_{t+1}, A_{t+1}\))

That’s SARSA: learning step-by-step from your real actions, even if your current “playlist” isn’t perfect.

Unlike Monte Carlo methods, which wait until the end of a full playlist (or episode) to update preferences, SARSA updates incrementally — after every song — using immediate feedback and your next action.

Illustration: SARSA

Pseudocode