7.2 On-Policy Function Approximation

What if you could estimate how good a move is — even when the board is too large to memorize? 🎯

Approximating state values is not sufficient to achieve control.

\[ \hat{V}(s; \mathbf{w}) \approx V_{\pi}(s) \]

Problem

What function should we focus on approximating in order to achieve control (approximate optimal policies \(\approx \pi_*\)) with continuous state information \(\mathbf{s}\)?

Example: MountainCar

Consider the following OpenAI Gymnasium MountainCar environment (Moore 1990):

Solution

Question 🤔

How can we summarize the Semi-Gradient SARSA update equation in 3 components?

\[ \mathbf{w}_{t+1} = \mathbf{w}_{t} + \underbrace{\alpha}\underbrace{(R_{t+1} + \gamma \hat{Q}(S_{t+1},A_{t+1}; \mathbf{w}_{t}) - \hat{Q}(S_{t},A_{t}; \mathbf{w}_{t}))}\underbrace{\nabla_{\mathbf{w}_{t}} \hat{Q}(S_{t},A_{t}; \mathbf{w}_{t})} \]

Answer

Off-Policy Function Approximation

Baird’s Counterexample shows that even with linear function approximation, off-policy TD methods like Q-learning can diverge.

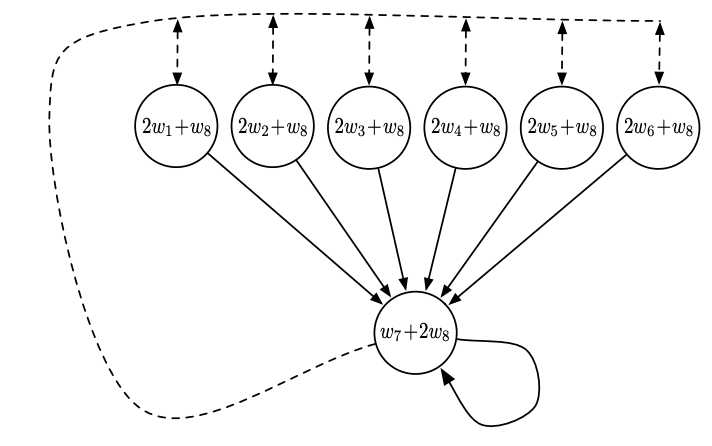
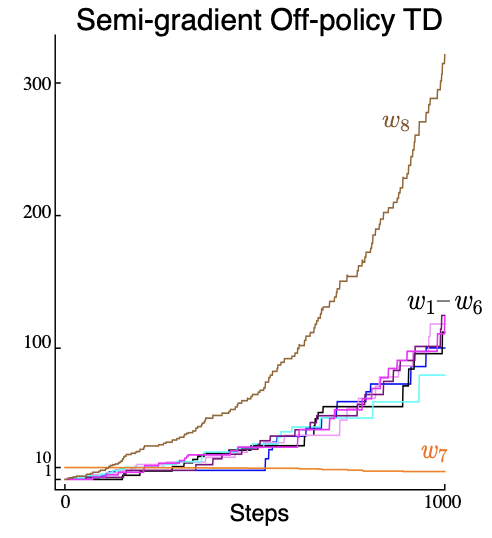
A real-world demonstration of this divergence: as training progresses, value estimates explode instead of converging.

Convergence of control algorithms:

Algorithm	Tabular	Linear	Neural Networks
Monte-Carlo Control	✅	(✅)	❌
SARSA	✅	(✅)	❌
Q-learning	✅	❌	❌