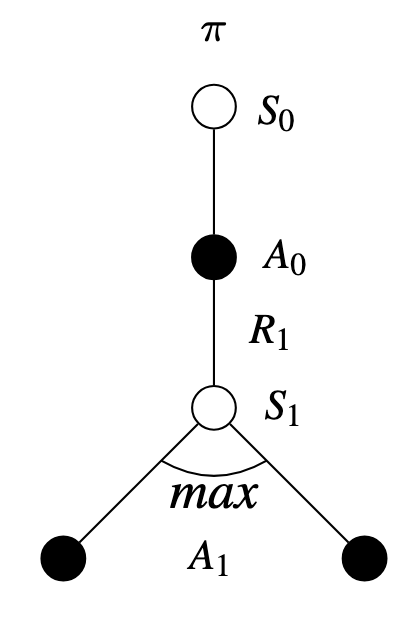
6.3 Q-Learning
Ideally, we would like to have a TD method that can be off-policy.
How can we leverage the Temporal Difference learning rule to approximate the optimal policy \(\approx \pi_*\) by learning from actions we didn’t take — using the best possible next action \(A\) to update our strategy, even if it wasn’t chosen by our current policy \(\pi\)?
Suppose you’re studying chess by watching a famous game between two grandmasters:
- \(S\) — You recognize a familiar board position from their match.
- \(A\) — In your current game, you’re unsure what to play — but you recall the grandmaster’s move in that same position.
- \(R\) — You remember that the move they chose led to a strong positional advantage (high reward).
- \(S'\) — You predict the next likely position on the board and evaluate the possible replies.
Even though you’re not playing exactly like the grandmasters did — and your opponent may respond differently — you use the best move from their game as your update target, trusting that it’s the optimal next action in that state.



You don’t have to repeat the entire grandmaster game — you just need to know what move worked best in each position and adjust your own strategy accordingly.
How can you improve your chess strategy by learning from the best moves of others — even if you never made those moves yourself?
Q-Learning is a TD off-policy method that can both update and estimate the optimal action-value function directly:
\[ Q(S_{t},A_{t}) = Q(S_{t},A_{t}) + \alpha [ R_{t+1} + \gamma \max_{a} Q(S_{t+1},a) - Q(S_{t},A_{t})] \]
Q-Learning is a breakthrough in reinforcement learning due to its simplification of algorithm analysis and early convergence proofs.
Illustration: Q-Learning