6.1 Temporal Difference (TD) Prediction
Monte Carlo is a powerful learning rule for estimating value functions \(v_{\pi}\) and action value functions \(q_{\pi}\) in associative environments.
The power of Monte Carlo resides in its ability to learn the dynamics of any environment, without assuming any prior knowledge, only using experience.
Monte Carlo methods are based on averaging sample returns of trajectories following a policy \(\pi\).
How can we design a learning rule that updates value estimates during an episode, rather than waiting until the entire trajectory \(\tau\) is complete?
Assume \(\gamma = 0.9\)
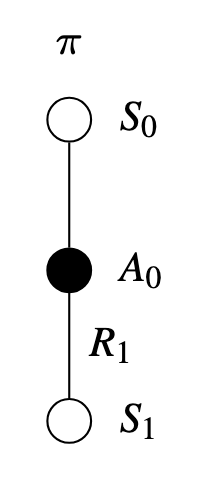
Suppose we follow the trajectory of \(\pi\) for one episode:
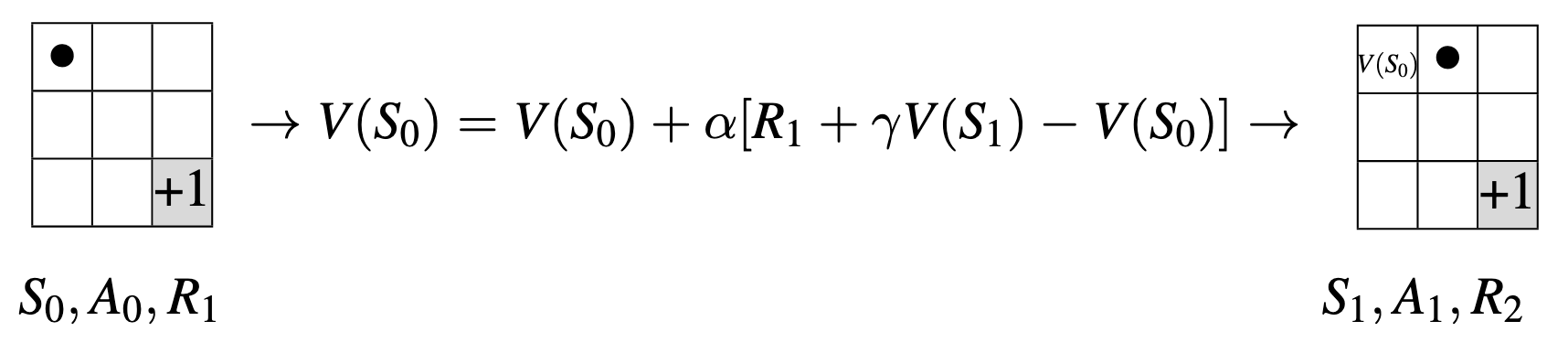
Temporal Difference (TD) is a learning rule that is a combination of Monte Carlo and Dynamic Programming ideas.
- TD methods, like Monte Carlo, learn from experience by updating estimates of nonterminal states along a trajectory \(\tau\).
- TD methods, like Dynamic Programming, update based on an existing estimate \(V(S_{t+1})\).
TD methods at time \(t + 1\) immediately form a target and make a useful update using the observed reward \(R_{t+1}\) and the estimate \(V(S_{t+1})\) in a incremental fashion:
\[ V(S_{t}) = V(S_{t}) + \underbrace{\alpha}_{Step \ Size} [ \underbrace{\underbrace{R_{t+1} + \gamma V(S_{t+1})}_{Target \ Update} - V(S_{t})}_{TD \ Error}] \]
Illustration: Temporal Difference (TD) Prediction