6.4 Double Q-Learning
The problem with relying with the conceptions of previous behavior \(b\) is that it is susceptible to biases.
How can we leverage the Temporal Difference learning rule to approximate the optimal policy \(\approx \pi_*\) by learning from actions we didn’t take — without falling into biases of conceptions of previous behavior \(b\)?
Much of classical economics assumes humans make perfectly rational decisions — but Daniel Kahneman’s Thinking, Fast and Slow revealed how our minds often fall into predictable biases.


Kahneman describes two modes of thought:
- 🧠 System 1 — Fast, automatic, emotional, and often biased; rooted in evolutionarily older brain structures like the limbic system, designed for quick survival decisions.
- 🧠 System 2 — Slow, deliberate, logical, and effortful; associated with the prefrontal cortex, which supports planning, reasoning, and self-control.
Which of the two lines is longer?
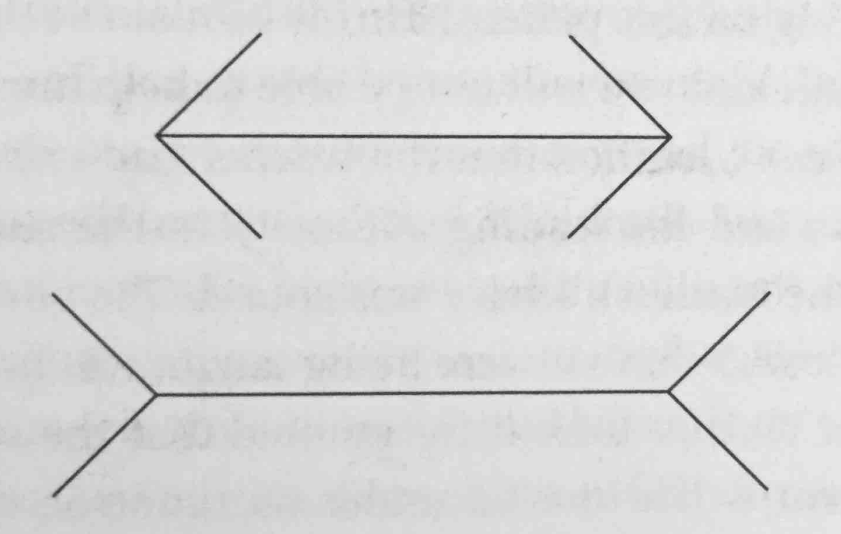
Answer: They are of the same length.
Imagine a pond that gets filled by an invasive species (like algae) that doubles in size every day. If the river becomes completely full on the 30th day, on which day was it half full?
Answer: Day 29.
How can keeping your fast, intuitive decisions in check with a slower, more reflective system help you avoid overconfidence — and make better choices over time?
Double Q-Learning addresses this bias by creating two action value estimates \(Q_{1}(s,a)\) and \(Q_{2}(s,a)\).
With equal likelihood, one action value estimate yields the maximization action \(A_{t}\) and the other provides the action value estimate \(Q(S_{t}, A_{t})\).
\[ Q_{1}(S_{t},A_{t}) = Q_{1}(S_{t},A_{t}) + \alpha [R_{t+1} + \gamma Q_{2}(S_{t+1},\max_{a} Q_{1}(S_{t+1},a)) - Q_{1}(S_{t},A_{t})] \]
\[ Q_{2}(S_{t},A_{t}) = Q_{2}(S_{t},A_{t}) + \alpha [R_{t+1} + \gamma Q_{1}(S_{t+1},\max_{a} Q_{2}(S_{t+1},a)) - Q_{2}(S_{t},A_{t})] \]
This dual-system model mirrors Double Q-learning:
- One Q-estimator (\(Q_1\)) makes a quick action selection — like System 1.
- The other Q-estimator (\(Q_2\)) does the critical evaluation — like System 2.
This separation reduces maximization bias, much like System 2 tempers System 1’s impulsive decisions.
Pseudocode
Maximization bias is a maximization of actual action value estimates \(Q(s,a)\) is higher than those of the true action values \(q(s,a)\), leading to a bias.