4.4 Value Iteration

What if you could leap straight to the best decision by updating values in one sweep? ⚡

Dynamic Programming is a collection of algorithms that can be used to compute optimal policies \(\pi_{*}\).

One drawback of policy iteration is that policy evaluation is done iteratively, requiring convergence exactly to \(v_{\pi}\) which occurs only in the limit.

Problem

Can we find a way to improve policies without waiting for full convergence of \(v_{\pi}\)?

Real Life Example 🧠

Imagine your commute to work every day:

\(S\) — The location you’re currently in (e.g., your home or a traffic junction). More generally, \(S_{1,...,k}\) can represent multiple possible locations.
\(A_{1,...,k}\) — The route you can choose (e.g., highway, back streets, scenic route, parkway, or alternate street).
\(R\) — Your reward could be getting to work quickly, stress-free, or on time.

Action \(A_1\): Choosing the highway from your current location \(S\). Reward \(R\): Travel time may vary depending on traffic, but contributes to the overall value of being in this state.

Action \(A_2\): Taking the side street from your current location \(S\). Reward \(R\): Usually a reliable route with moderate travel time, contributing to the value of this state.

Action \(A_3\): Taking the parkway from your current location \(S\). Reward \(R\): Might have moderate traffic but pleasant scenery, adding to the state value.

Action \(A_4\): Using an alternate back road from your current location \(S\). Reward \(R\): Unfamiliar route, so contribution to state value is uncertain.

Suppose you want to find the optimal route from home to work. Rather than just trying one alternative, you evaluate all possible routes from each location, estimate the expected travel time (or reward) recursively, and keep updating your estimates until they converge.

How could you systematically assign a value to each location and decide which route maximizes your overall commute reward?

Solution

Value Iteration truncates the policy evaluation step after just one sweep.

Generalized Policy Iteration

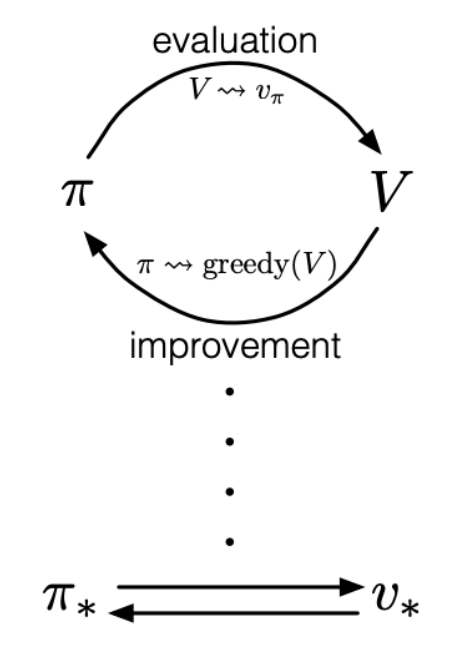
Generalized Policy Iteration (GPI) refers to the general idea of letting policy evaluation and policy improvement processes interact, regardless of anything else.

Almost all of Reinforcement Learning can be described as the policy always being improved with respect to the value function, and the value function always being driven toward the value function for the policy.