5.1 Monte Carlo Prediction
Dynamic Programming is a collection of algorithms that can be used to compute optimal policies \(\pi_{*}\).
These algorithms have limited utility in Reinforcement Learning due to:
- Assumption of a perfect model: All state transitions \(P(s', r \mid s, a)\) are known in advance.
- Computational expense: Dynammic Programming typically requires full sweeps over the state space \(\forall s \in S\), which is only feasible in small, tabular environments.
How can we find an optimal policy \(\pi_{*}\), assuming that we have no prior knowledge of state transitions \(P(s', r \mid s, a)\)?
Assume \(\gamma = 0.9\)
Suppose we followed the trajectory of \(\pi\) for one episode:
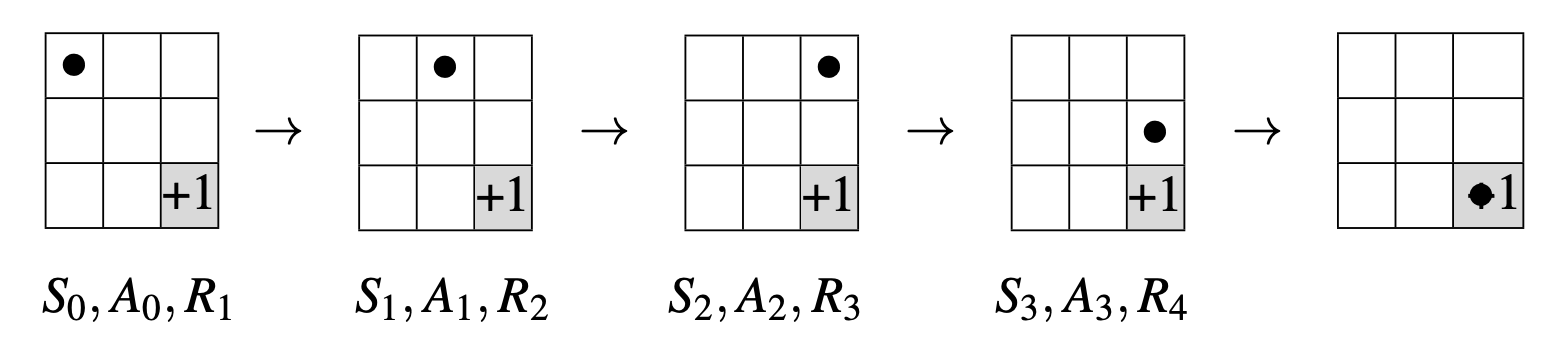
The following illustrates a Monte Carlo update for the trajectory:
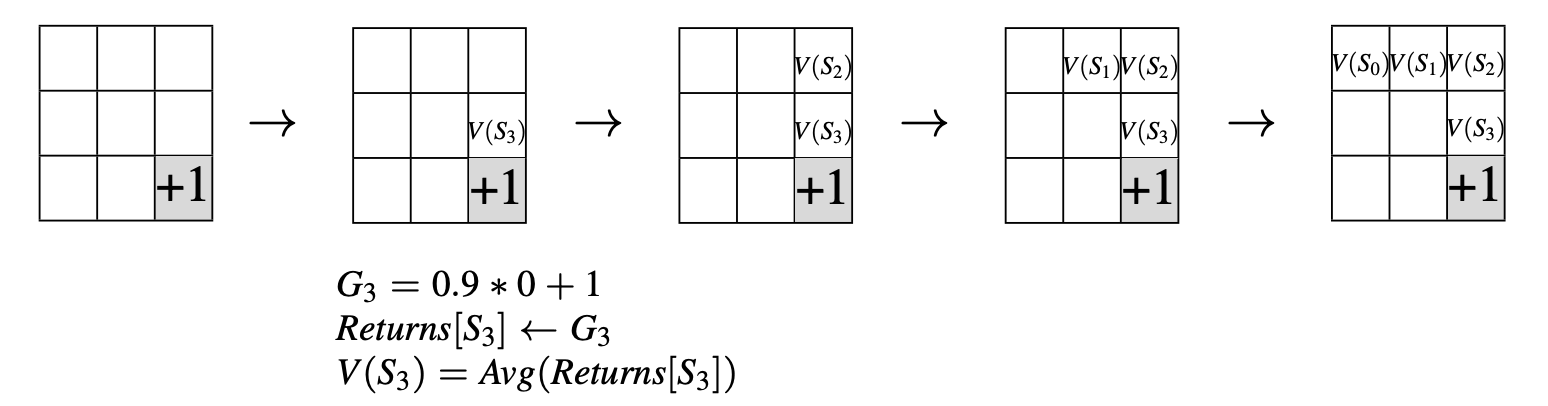
Monte Carlo is a powerful learning rule for estimating value functions \(v_{\pi}\) and action value functions \(q_{\pi}\) in associative environments.
The power of Monte Carlo resides in its ability to learn the dynamics of any environment, without assuming any prior knowledge, only using experience.
Monte Carlo methods are based on averaging sample returns of trajectories following a policy \(\pi\).
Only on the completion of an episode are value estimates \(v_{\pi}(s)\) and action value estimates \(q_{\pi}(s,a)\) updated.
Illustration: Monte Carlo Prediction
Pseudocode
Recall that returns are calculated as follows:
\[ G_{t} = r_{t+1} + \gamma G_{t+1} \]